Regime Changing detection is useful in many cases, including finance, economics, climate science, and engineering.

  • Financial Market Analysis:

Helps identify shifts in market trends (e.g., bull vs. bear markets). Improves trading strategies by adjusting risk management based on detected changes. Can be used to detect changes in volatility, correlation, or liquidity. Algorithmic Trading & Quantitative Finance:

Useful for adapting trading algorithms when market conditions change. Helps optimize stop-loss and take-profit levels by recognizing trend shifts.

  • Risk Management:

Detecting regime changes in asset returns or volatility helps adjust portfolio strategies. Avoids unexpected losses due to abrupt changes in market behavior. Macroeconomic and Business Cycle Analysis:

  • Identifies economic phase transitions (e.g., recession vs. expansion).

Helps policymakers and businesses adjust strategies accordingly. Time Series Forecasting:

  • Improves predictive accuracy by accounting for structural changes.

Avoids overfitting models to past data that may no longer be relevant. Climate and Environmental Science:

  • Detects shifts in climate patterns, such as global warming trends.

Helps in early warning systems for extreme weather events. Industrial Monitoring & Quality Control:

Identifies shifts in system performance or failure modes. Helps in predictive maintenance by detecting early signs of wear or malfunction.

Simulation

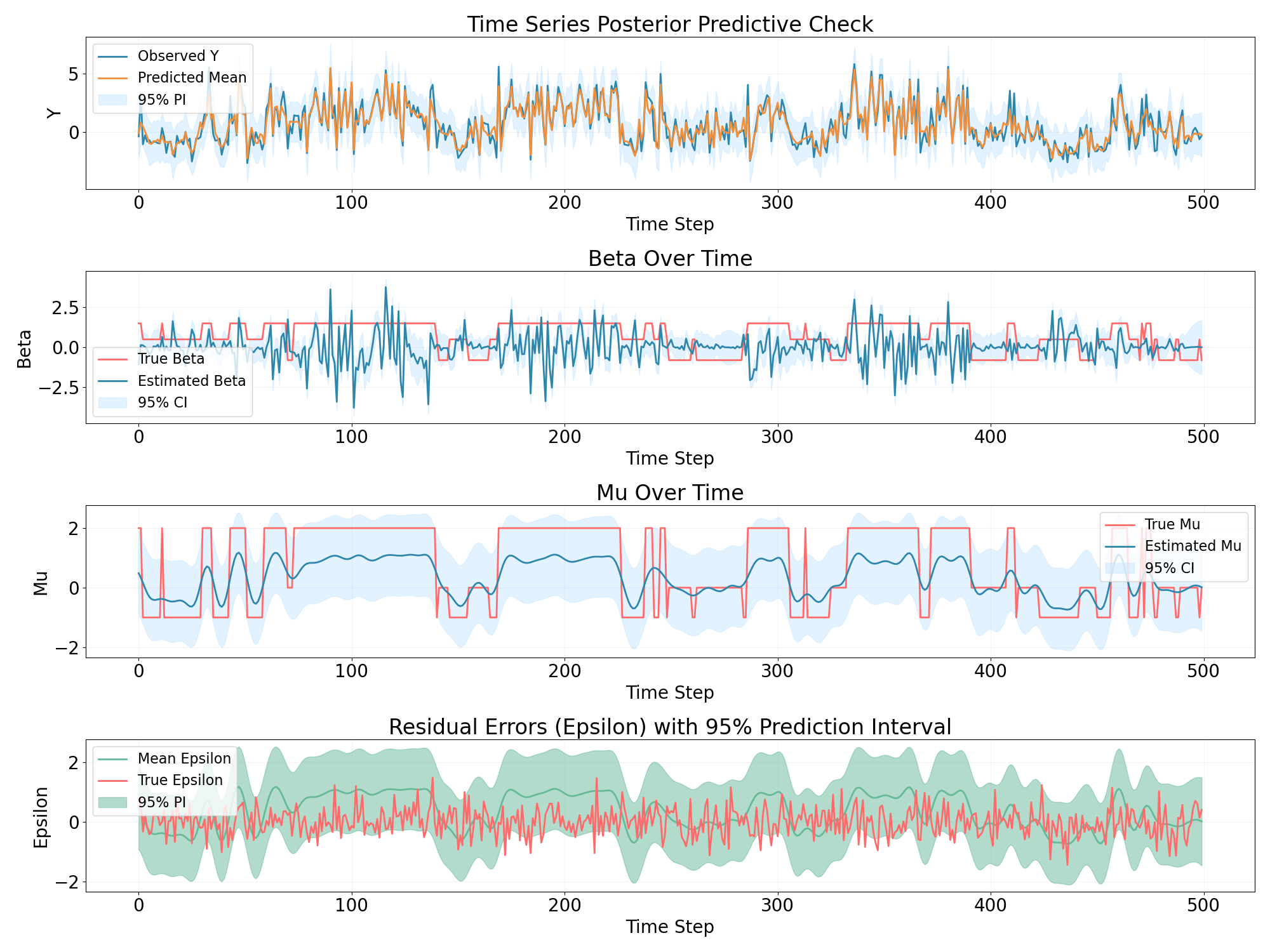
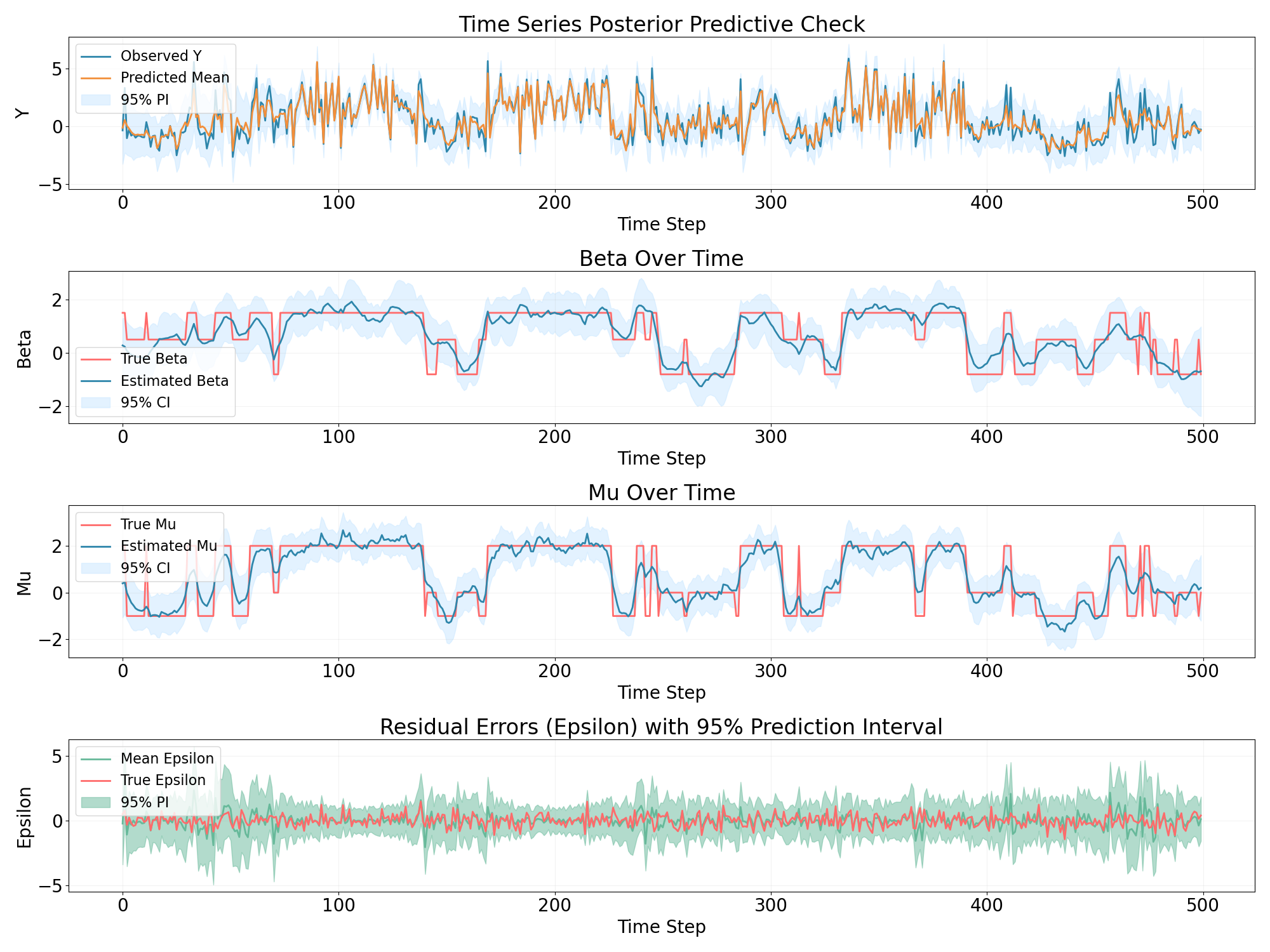
The regime changing is described in the following state space mode:

$$Y_t = β_tX_t + \mu_t + ϵ_t $$

Where the $\beta$ and $\mu$ are time verying.

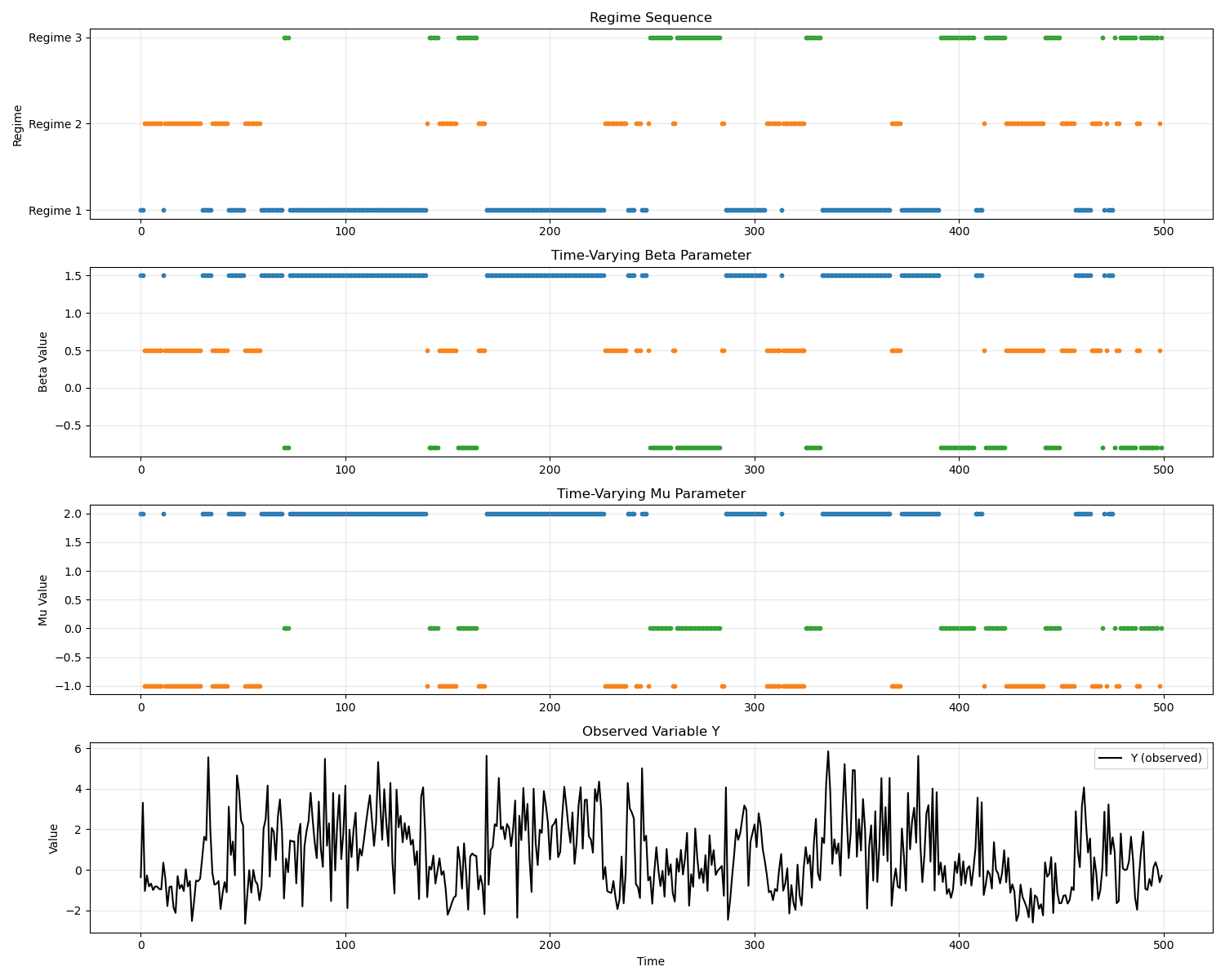
Here we have a data generating process that has a regime changing behavior: 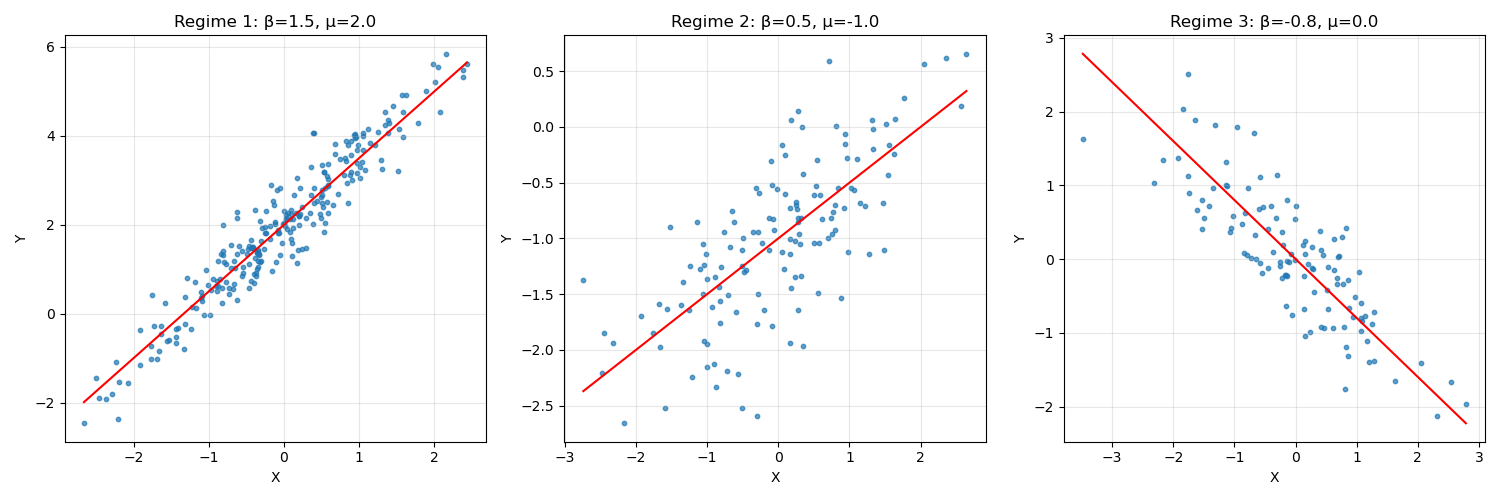img.png And we use these three regimes to generate a time series by random choices of the regimes: img.png

And then we use the four models that were described in the previous post:

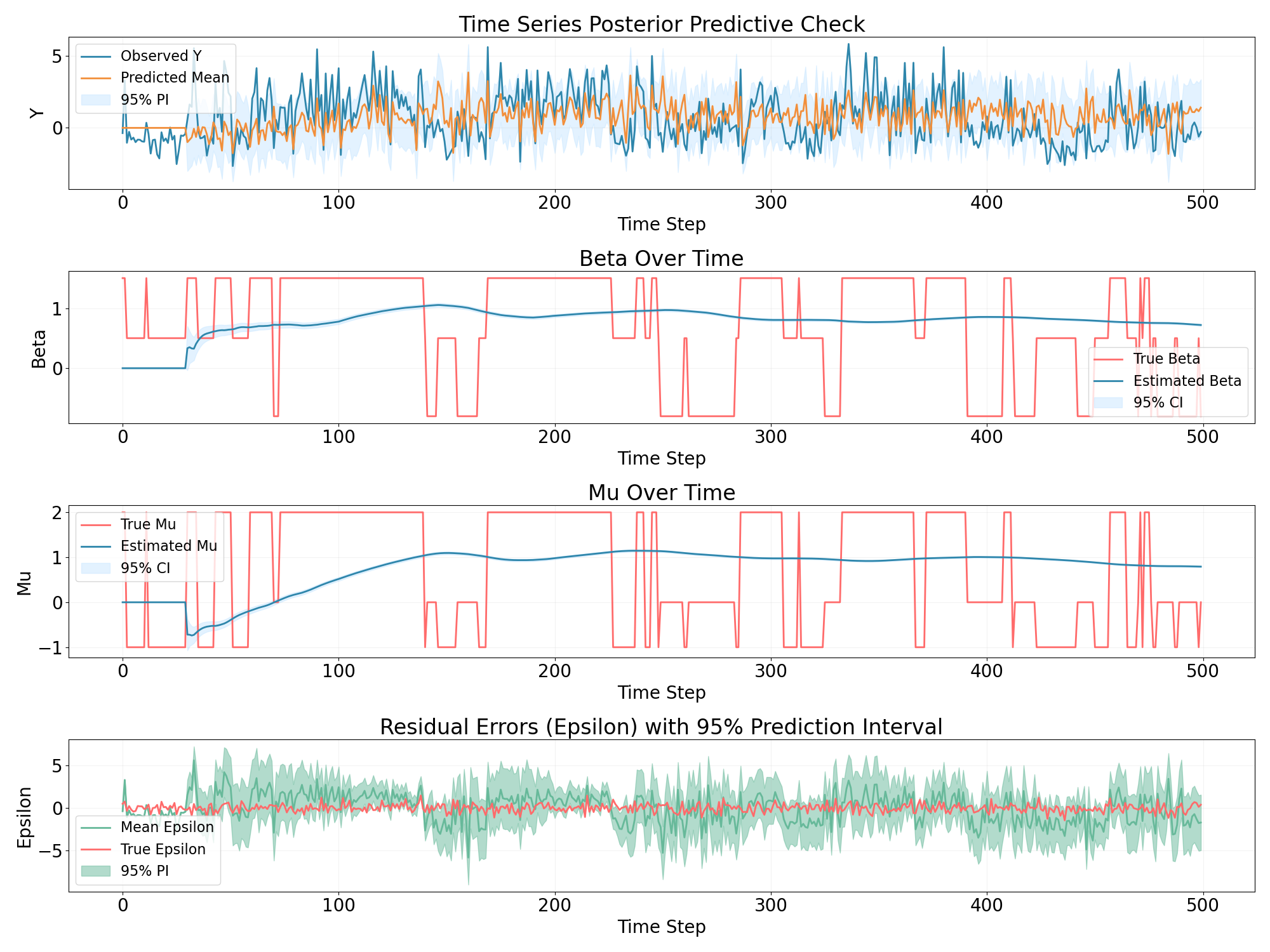
  • rolling window regression img.png

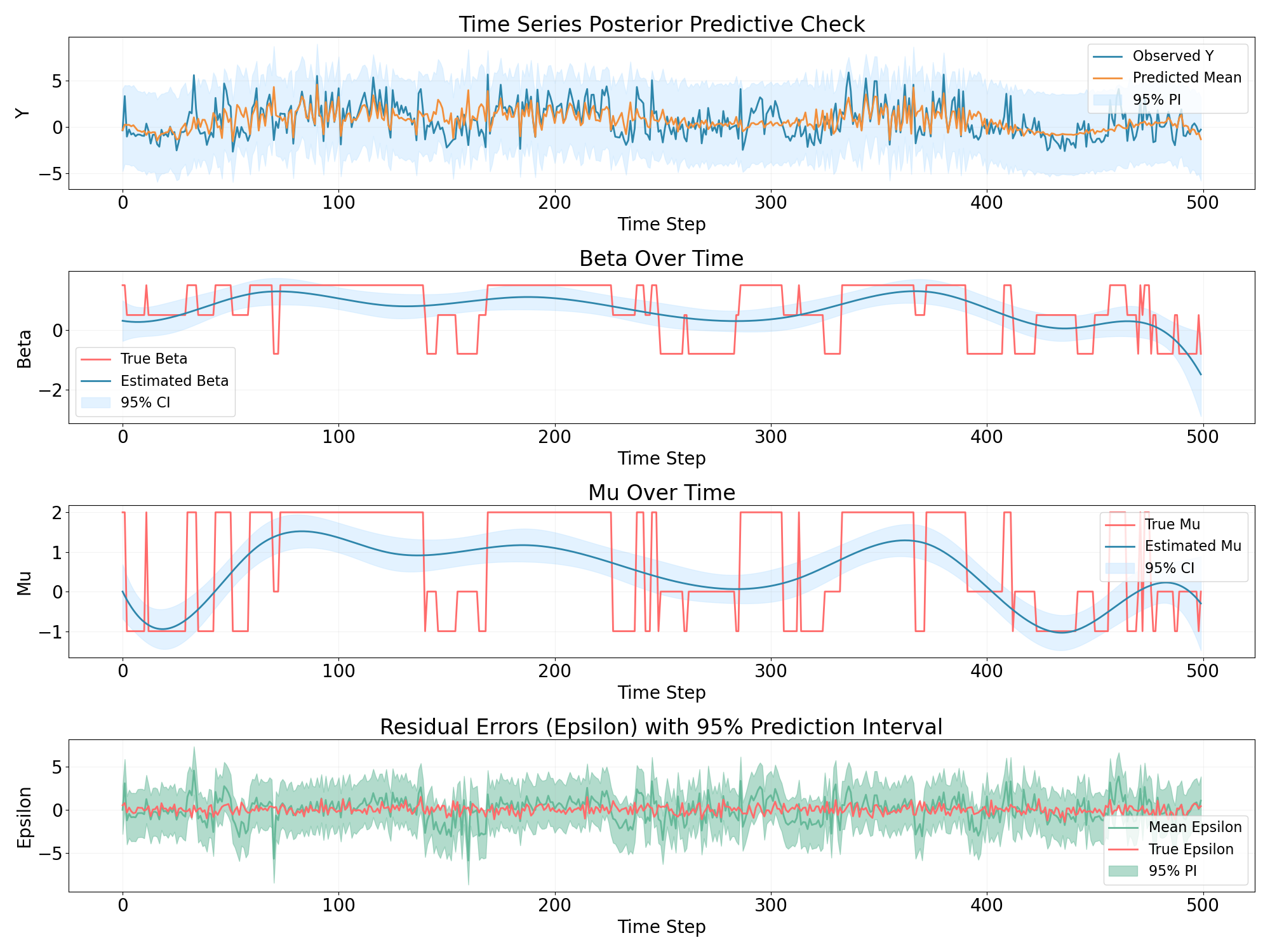
  • Bayesian GAM img.png

  • Composite Gaussian Process img.png

  • Bayesian structural time series img.png

  • Conclusion

It seems that the simple model such as rolling window regression and GAM couldn’t capture the discontinue time verying states well.

In this case the BSTS model works the best.